导语:正65537边形具有65537条边,65537个顶点,利用肉眼观察它,看起来几乎就是一个圆,所以它也是边数为质数的多边形中,能用尺规画出来的边数最多的多边形,一位叫做盖尔美斯的德国人,利用整整10年的时间做出了真正的正65537边形,下面就跟着探秘志小编一起来看看吧!
最奇葩多边形:正65537边形
虽然正65537边形是多边形的一种,但是由于边数特别的多,足足有65537条,所以很多人都会将它误解为一个圆。光是它的顶点就有65537个,内角和也是无比的大,达到了11796300度,所以单是用普通的尺规可能要画到天荒地老,才能画出完整的正65537边形。
正65537边形虽然看起来十分简单,但是它的面积和边长的计算确实十分复杂的,据资料显示,一个半径为1的圆就能通过内切达到正65537边形的状态,所以它的大致面积数值应该与圆周率十分相近,边长也不是那么好算的,如果和半径为1的圆作对比,正65537边形的边长大约是0.000095872336310378200520953689053403,看起来着实有些吓人。
用尺规如何画出正65537边形?
与毕达哥拉斯树不同,正65537边形并非人人都有耐心画出来,但是早在1801年高斯出版的《算术研究》中,就证明了正P边形是可以用尺规画出来的,只要P是费马数,而正好65537就是第五个费马数,所以是能够用尺规画出来的,而且也是在边数为质数的多边形中,能用尺规画出来的边数最多的多边形。
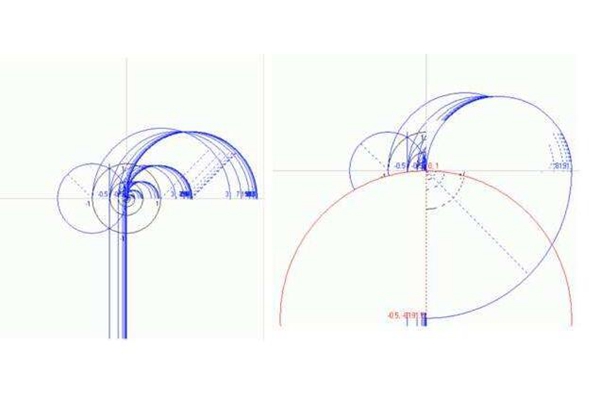
但是关于正65537边形的具体尺规作图方法,高斯并没有阐述,其实利用最原始的尺规手绘作图,必然是一项浩大的工程,不过也曾经有一位叫做盖尔美斯的德国人,利用整整10年的时间做出了真正的正65537边形,据说当时的手稿就装满了一整个手提箱,现在还保存在哥本哈根大学内。
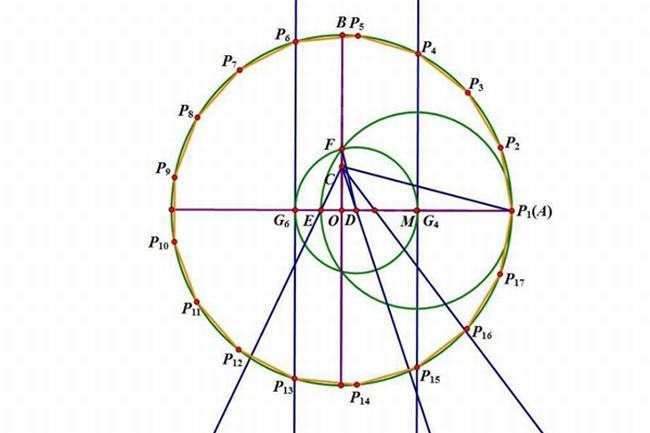
当然目前为止最简单的正65537边形的作图方法,可能就是直接画一个圆,再稍微做一下内切,并标上正65537边形,这也是最重要的一部,因为正65537边形和圆实在太像了,不仔细看,根本没有谁能看出区别,是不是很有意思了。
结语:正65537边形就像世界上最神奇的数字一样奇葩,数学中还有不少有趣的现象,这也给人们带来了不一样的科学感受。
导语:Szilassi多面体就是七面体的一种,有着一个180度的对称轴,属于拓扑结构中的环,被归为凸多面体之中,大约有7个六边形组成,其中的六个面都是凸六边形,每个相邻的面都有共用边,下面就跟着探秘志小编一起来看看吧!
Szilassi多面体是什么?
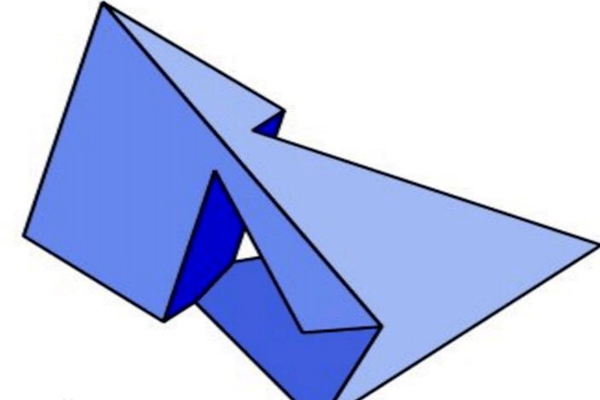
其实Szilassi多面体就是七面体的一种,属于拓扑结构中的环,被归为凸多面体之中,大约有7个六边形组成,其中的六个面都是凸六边形,每个相邻的面都有共用边,虽然Szilassi多面体长的很奇怪,但其实它是个对称立方体,并且有着一个180度的对称轴。
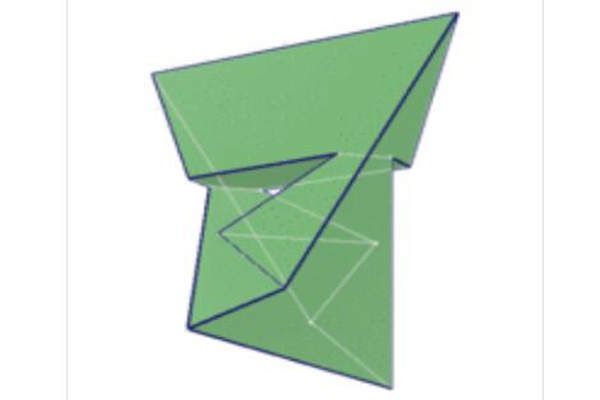
Szilassi多面体之中有三组面全等,且可以运用七种颜色涂满每个相邻的面,也就成了七色定理的最低限,七色定理就是说在亏格为一的环面上染色,必须要7种颜色。Szilassi多面体具有14个顶点和21条边,也是目前已知的每个面都与其他面公用边的多面体之一,还有一个被叫做Heawood graph的四面体,也具有同样的属性。
Szilassi多面体展开图长什么样?

上图就是Szilassi多面体的每个面的投影视图,也就是相当于三视图的感觉,通过这四张图就能大致的感受到Szilassi多面体的样子,比如第二张图就是从侧面看到的样子,而最后一张图就是从顶部看到的样子。

这里是Szilassi多面体的旋转图,能方便看到的更加清晰,对结构更加明了,其实这样看来就像两个三角体互相交叉,并在中间挖出了一块,和正六百胞体不同的是,Szilassi多面体很是比较容易理解的,而且看上去很对称,并不像它的四视图中看到的那么奇怪。
七面体是什么?

其实也就是由七个面组成的多面体,比较常见的有六角锥和五角柱,而Szilassi多面体也是其中一种,不像其他的偶数多面体,由于七是单数,所以根据欧拉公式显示,正七面体是不存在的,因为7不能被整除。
结语:Szilassi多面体虽然不是一个常见的七面体,但也让人们看到了数学的独特,其实数学的趣味性经常表现在几何方面,比如毕达哥拉斯树就是其中一种。