导语:等腰三角形悖论是说所有的三角形都是等腰三角形,但是这一悖论显然是错误的,因为我们很容易做出一条边长分别为3,4,5的三角形,利用反证法就能推导出错误,下面和探秘志了解一下。
等腰三角形悖论
所谓的等腰三角形悖论就是一个有关等腰三角形的悖论,主要内容是,所有的三角形都是等腰三角形。先不说结果如何,来说说悖论本身。相信很多人都知道学过有三角形的知识,大家不仅见过等腰三角形也见过不等腰的三角形,但是问题是应该怎样来验证悖论真实与否呢?毕竟之前的钱包悖论、生日悖论和费米悖论都是经过了一定的验证的。
该悖论的相关说法

命题:假如有一个三角形,那么这个三角形就是等腰三角形。
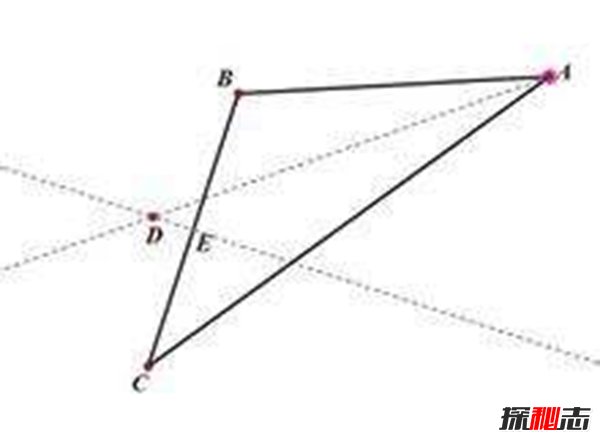
论证:在一个三角形[db:tags]BC中,E是∠A的角平分线和BC垂直平分线的交点,F和EG垂直于边AB,而AC的垂足是F,G。比较容易的可以得出△AEF≌△AEG(AAS),△EFB≌△EGC(HL)。然后就有AF=AG,BF=CG,所以AB=AC,最终得出结论三角形ABC是等腰三角形。
这个论证乍一看去相当有理有据啊,但是这个说法真的是正确的吗?假如不正确错误的地方在哪里呢。

问题的关键:实际上E点的位置一直都在三角形的外面而不是里面,只要大家正确的做一个图就知道了。
结论:因为在△ABC中,E是∠A的角平分线和BC垂直平分线的交点,但是根据画图可以知道,不管是锐角、直角还是钝角三角形,点E都在△ABC的外面。所以最终这条悖论就迎刃而解了。
这条悖论就是乍一看去很像那么回事,仔细想想总有那么些奇怪,最终靠正确作图就能找到问题的症结所在。另外大家也可以比较容易的做出一个三条边分别为3,4,5的三角形,这个说法实在不能更假了。
结语:不管是在生活中还是在数学世界中都有这样或者那样的讨论,悖论也算是比较重要的一种只有提出质疑最终才能进步。
导语:麦克斯韦妖是世界著名物理学家詹姆斯·麦克斯韦提出的猜想,假如有一个密闭的容器,阀门妖怪控制着高速分子和慢速分子的开关,主要是为了说明热力学第二定律的可能性,但这只是理想中的存在,科学家认为麦克斯韦妖在控制门的过程中会进行一些消耗,不可能永动下去,下面探秘志带大家了解一下。
麦克斯韦妖什么意思
麦克斯韦妖是世界十大著名物理学家之一詹姆斯·麦克斯韦提出的猜想,主要为了说明热力学第二定律的可能性而提出的设想。
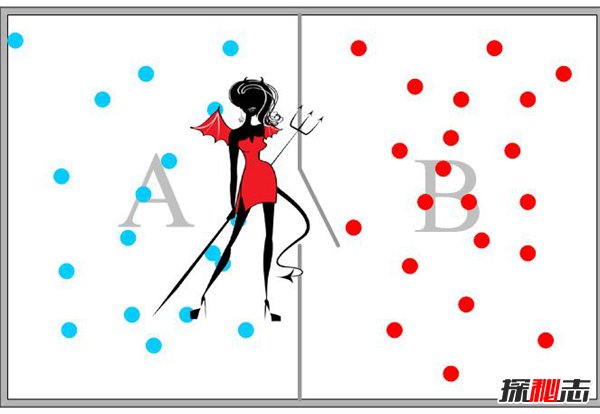
在1871年物理学家为了研究相关的理论,提出了一个有意思的猜想,假如有一个密闭的容器,中间一个没有任何摩擦力的板子将其分成AB两部分,而在隔板上面有一个妖怪控制的阀门。

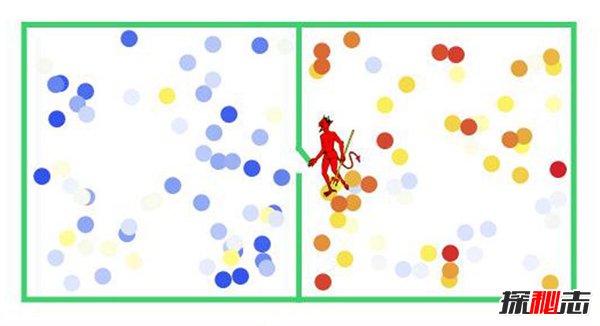
最开始两边的温度一样,当高速分子由A向B运动或慢速分子由B向A运动时,妖怪就会把门打开。而当当高速分子由B向A运动或慢速分子由A向B运动时,妖怪就会把门关上,最终久而久之所有的高速分子都会到达B区,而所有的慢速分子都会来到A区,这个系统就会变得更加有序。
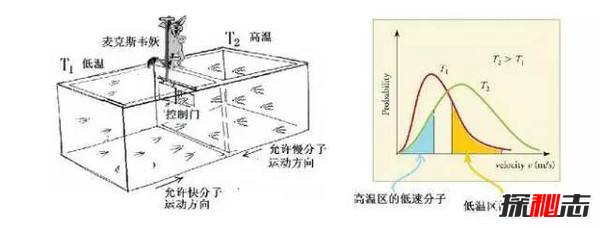
后来法国物理学家L.布里渊在1956年中发表的相关书籍中也提到了麦克斯韦妖,他认为因为容器是密闭的比较孤立的空间,在相当黑暗的地方,即使是妖怪也不能看到任何东西,所以也没办法更好的了解什么是高速分子,什么是低速分子。
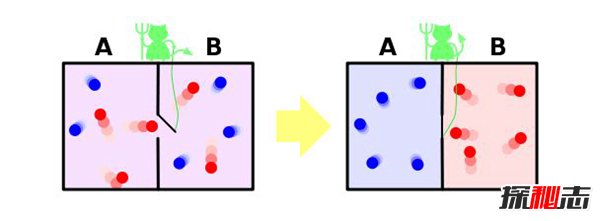
麦克斯韦妖只有在获取更多的相关信息和能量才能真正的开始工作,不过所谓的麦克斯韦妖也是理想中的存在。
麦克斯韦妖和永动机
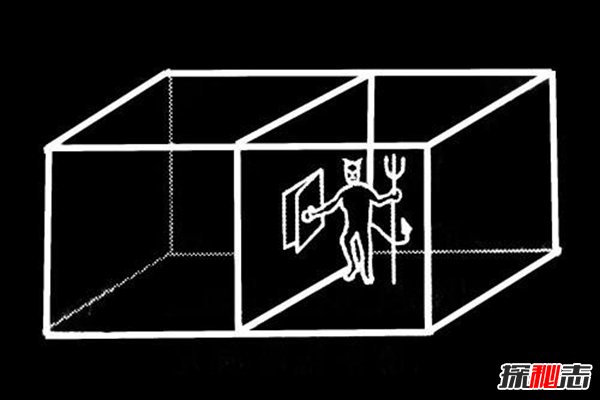
什么是永动机,这是一种理想中存在的产物,因为不需要任何的外界输入就可以一直运动下去,而麦克斯韦妖和永动机有着异曲同工之妙。但是后来有科学家认为麦克斯韦妖在控制门的过程中会进行一些消耗,并不可能永不停歇的进行下去,所以永动机的相当也是不可能实现的。而黄油猫悖论也只是一种悖论而已并没能真正实现。
结语:麦克斯韦妖实际上就是在物理中提出来的一种猜想,主要是为了证明某些理论,但是事实证明这种猜想是错误的,不过其猜想的过程还是比较值得考究的。






