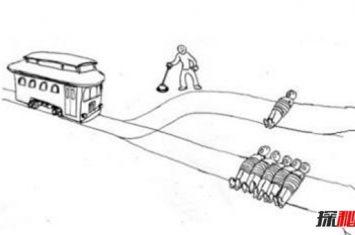
导语:大家有没有这样的情况,对着某个比较亮的东西看久了,移开目光依旧感觉看到了刚刚的东西,这就是所谓的视觉残像,有很多网上所谓奇怪的图片都是利用这一点来进行操作的,感觉这个比较有趣,和波根多夫错觉有的一拼,下面和探秘志小编一起了解一下吧。
视觉残像

眼睛在经过强光刺激后,会有影像残留于视网膜上,这是由于视网膜的化学作用残留而引起的,这就是残像。残像的问题主要是影响观察,因此应尽量避免强光和玄光的出现。
基本含义

从生理学角度来讲,物体对视觉的刺激作用突然停止后,人的视觉感应井非立刻全部消失,而是该物的映像仍然暂时存留,这种现象称作视觉余像“。视觉余像分为正余像和负余像两类。视觉余像的形成,是眼睛连续注视的结果,是因为神经兴奋所留下的痕迹而引发的。当外界物体的视觉刺激作用停止以后,在眼睛视网膜上的影像感觉并不会立刻消失,这种视觉现象叫做视觉后像。视觉后像的发生,是由于神经兴奋所留下的痕迹作用,也称为视觉残像。
残像对影视技术与传播设计来说具有非常重大的意义。正由于视觉残像的作用,才使我们有幸欣赏电影与动画艺术。正由于残像作用,使我们能通过移动的狭缝看清隐蔽其后的形象,也就是实现形象的非同时拼接。这正是电视成像的根本原理。残像是视觉后效之一
产生的原因

当我们的眼睛长时间的看着红色,然后转向百墙的时候,会感觉白墙上有绿色。这就是所谓的视觉残像。发生这种情况的原因是:当红色辐射光刺激人眼的感觉细胞时,会产生神经兴奋,而视线转移后,由于兴奋神经和抑制神经相互诱导的作用,使原来兴奋的神经处于抑制状态,而感受绿色的细胞反而兴奋起来,从而感到白墙上有绿色。
结语:残像在生活中很多地方运用的比较广,尤其是在动画领域更是特意利用了这些,感兴趣的朋友可以继续去了解更多哦。
导语:牟合方盖听名字是不是非常陌生,这是我国古代数学家刘徽发现的一种用于计算球体体积的方式,他希望可以用牟合方盖来证实《九章算术》的公式有错误,虽然最终并没有实现,但是这个发现有着重要的意义,下面和探秘志小编一起看看吧。
牟合方盖

这是我国古代数学家刘徽首先发现并采用的一种用于计算球体体积的方法,类似于现在的微元法。由于其采用的模型像一个牟合的方形盒子,故称为牟合方盖。
基本理论
其实刘徽是希望构作一个立体图形,它的每一个横切面皆是正方形,而且会外接于球体在同一高度的横切面的圆形,而这个图形就是“牟合方盖”,因为刘徽只知道一个圆及它的外接正方形的面积比为π:4,他希望可以用“牟合方盖”来证实《九章算术》的公式有错误。当然他也希望由这方面入手求球体体积的正确公式,因为他知道“牟合方盖”的体积跟内接球体体积的比为4:π,只要有方法找出“牟合方盖”的体积便可,可惜,刘徽始终不能解决,他只可以指出解决方法是计算出“外棋”的体积,但由于“外棋”的形状复杂,所以没有成功,无奈地只好留待有能之士图谋解决的方法:
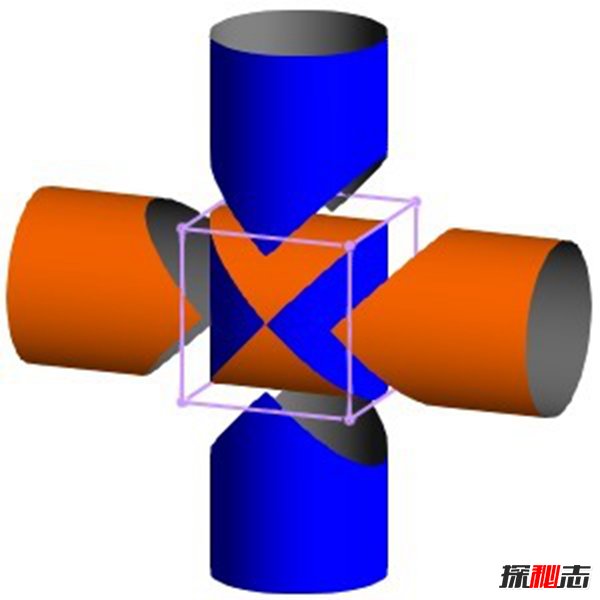
“观立方之内,合盖之外,虽衰杀有渐,而多少不掩。判合总结,方圆相缠,浓纤诡互,不可等正。欲陋形措意,惧失正理。敢不阙疑,以俟能言者。”
但是在刘徽后二百多年贤能之士才出现,这就是中国伟大数学家袓冲之和他的儿子祖暅,他们继承了刘徽的想法,还利用了“牟合方盖”彻底地解决了球体体积公式的问题。
重要发现

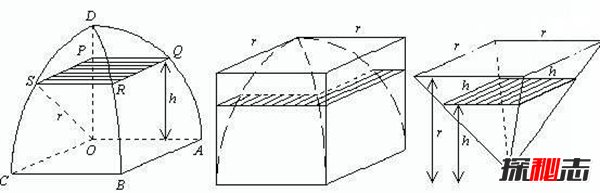
主要是使用的三个“外棋”的计算方法。他们先考虑一个由八个边长为r的正立方体组成的大正立方体,然后用制作“牟合方盖”的方法把这大正立方体分割,再取其中一个小正立方体部分作分析,分割的结果将跟右图所示的相同,白色部分称为“小牟合方盖”,它的体积为“牟合方盖”的八分之一,而紫红、黄和青色的部分便是三个“外棋”。

祖冲之父子考虑这个小立方体的横切面。设由小立方体的底至横切面高度为h,三个“外?”的横切面面积的总和为S及小牟合方盖的横切面边长为a,因此根据“勾股定理”有:
a²=r²-h²
另外,因为
S=r²-a²
所以
S=r²-(r²-h²)=h²
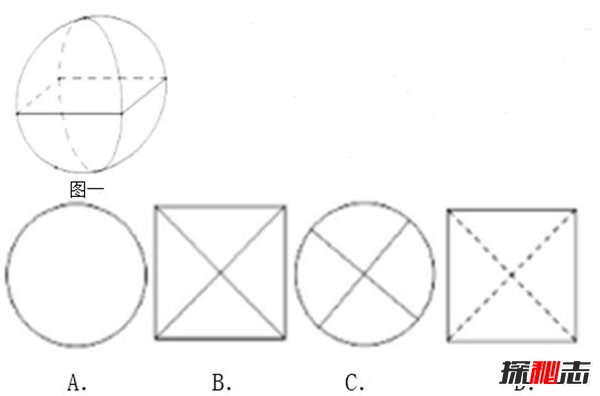
于所有的h来说,这个结果也是不变的。祖氏父子便由此出发,他们取一个底方每边之长和高都等于r的方锥,倒过来立着,与三个“外棋”的体积的和进行比较。设由方锥顶点至方锥截面的高度为h,不难发现对于任何的h,方锥截面面积也必为h²。换句话说,虽然方锥跟三个“外棋”的形状不同,但因它们的体积都可以用截面面积和高度来计算,而在等高处的截面面积总是相等的,所以它们的体积也就不能不是相等的了,所以祖氏云:
“缘幂势既同,则积不容异。”
所以
外棋体积之和=方锥体积=小立方体体积/3=r³/3
即
小牟合方盖体积= 2r³/3
牟合方盖体积=16r³/3
因此
球体体积=(π/4)(16r³/3)=4πr³/3
这条公式也就是正式的球体体积公式。
结语:牟合方盖是中国古代人民智慧的结晶,学习这些才能更好的了解数学知识,并且达到触类旁通的效果。