在宗教中几乎都是将上帝看作万能,但是曾经有人反驳让上帝造一块自己无法拿起的石头吧”,这就是著名的上帝悖论,但其中也有不少人指出它是存在漏洞的,宗教主义者的说法是认为你不是上帝你怎么知道上帝无法造出,要知道蚂蚁也不知道莫比乌斯环是立体的,而无神论者则表示这只是一种反证法,假定上帝是万能的,于是就找出反例来验证上帝不是万能。
上帝悖论是什么

作为世界十大悖论之一的上帝悖论,出处据说有两种说法,一是文艺复兴时期,有人文主义者用这个理论来抨击宗教主义者,以此来验证上帝不是万能的,因为无论是回答上帝造的出一块自己无法搬动的石头,还是回答造不出,都说明上帝并不是无所不能。而另一种说法则是来自于一位智者对于罗马教廷的抨击。
上帝悖论逻辑上的漏洞

首先如果从宗教上来说,有教徒认为上帝并非是同一个人,是一分为二的,如果一号上帝造出的石头搬不动,那么二号上帝就能来进行搬运,在这种前提下并不算是逻辑悖论。而且有人指出从《圣经》中表述的“上帝是无法撒谎的、是公正的、是友爱的”,因此也就意味着上帝虽然是万能的,但有些事情也是不被允许做的。

如果是从科学逻辑上来说,让上帝造出一块自己搬不动的石头,这其实就是在验证“上帝不是万能的”这一结论,而“搬不动的”这一限定词本身就是与万能上帝的前提是冲突的,就好比让上帝变出装水的空杯,本身就是为了反对而反对,而这就导致了这个悖论本身就是无意义的问题。

而且实际上就算是我们乍一看非常矛盾的事物,其实加上限定条件后也会变得相同,比如正方形的园其实是存在的,因为圆就是边长为零的正方形。而且上帝是可以在造出这块石头的时候,将其设定为搬不动,但是在之后秉持着上帝是万能的原则,他可以提高自己的力量从而举起石头。
贝特朗曾经在1899年提出了一个悖论就是,假设一个内接圆的等边三角形中,任意选择一条弦,那么这条弦长于等边三角形边长的几率有多大?但结果却并不是唯一的,分别利用三种方法解答出了二分之一、三分之一和四分之一,可以说它们都完全正确但相互矛盾,因此就形成了一个悖论。
贝特朗悖论正确答案
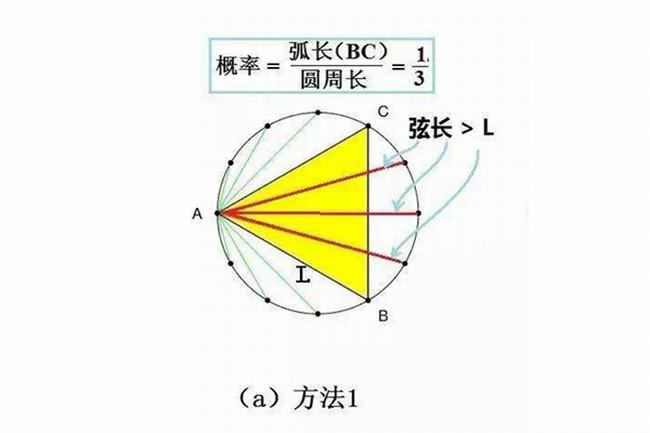
贝特朗悖论中并没有规定弦的位置、方向等,所以一共可以分为三种情况进行解答,第一种解法是先预设弦的方向,可以做出垂直于这条弦的直径,而计算出只有交于直径的四分之一和四分之三处的弦才是等于边长的,因此计算出概率为二分之一。而第二种方法则是预设了弦的一端,只有当弦与这个端点的切线交角为60-120度的时候才能等边,而概率就是三分之一。
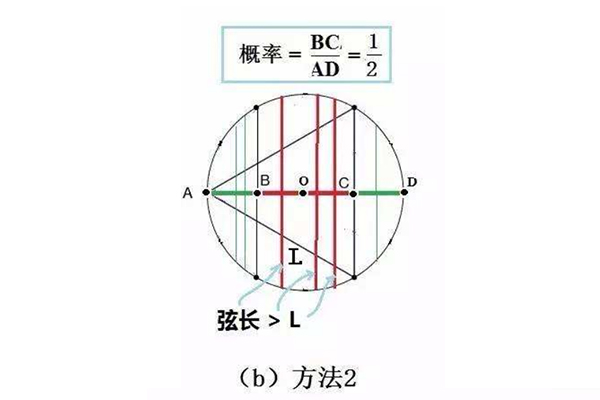
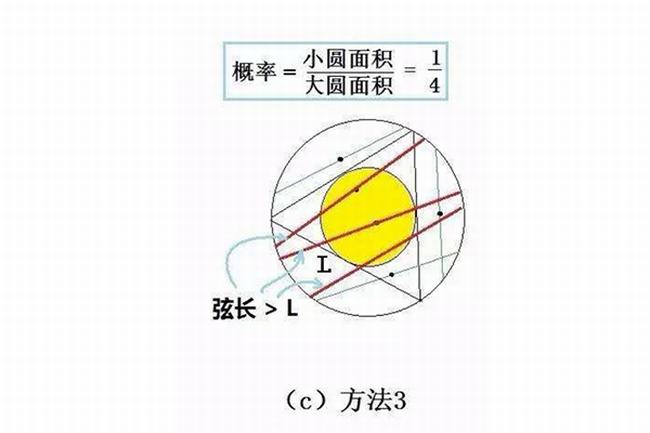
当然还有第三种解法,也是目前课本中最常用的解法,主要是根据弦的中点来看,只有弦的中心点能够落在比本圆半径小一半的同心圆上就能等长,因此这时的概率则只有四分之一。所以三种结果都不相同,但几乎都没有计算错误,其实也都是因为它的前提是不同的,在出题的时候,其中“等可能”的词汇会产生误导,这其实和芝诺悖论有得一拼。
贝特朗悖论的类似解释
其实这一悖论就是最初贝特朗用来反思几何学运算概率学到底是否合适的,其实这一悖论还有另外的一种版本。假设有1、2、3号箱子,其中1号有2根金条,2号有两根银条,3号有1根金条1根银条,打开一个隔间是金条,而打开另一个隔间也是金条的概率有多少?相信一般人都会认为是二分之一。

但实际上正确答案却是三分之二,因为我们可以看到2号箱子中只有银条,所以可以立即将它排除掉,而只剩下另外的1号和3号是有可能的,所以总的来说应该是三个箱子中有两个是可能的,所以这也是贝特朗悖论中最为简单的一个理解方式。






