导语:不可能图形是一种只能在二维世界存在的图形,属于一种典型的视错觉现象,是由于人类视觉对二维图形的三维投影出现了光学错觉导致的,不可能图形在三维世界中是不可能存在的,下面就跟着探秘志小编一起来看看不可能图形吧!
不可能图形是什么?
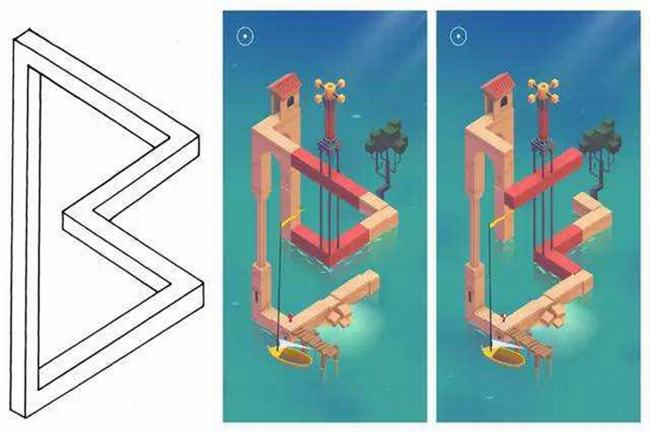
不可能图形其实就是一种视错觉,是人类视觉对一个二维图形的三维投射,都不可能在三维空间中存在,就像纪念碑谷中的那些诡异的图形链接,实际上都是视觉系统的错误判断,就像艾宾浩斯错觉一样,这样的图形其实还有很多,比如无尽阶梯,彭罗斯三角形等。

不可能图形的最先提出者是莫里茨科内利斯·埃舍尔,他是著名的视错觉画家,他的画作中大部分都是此类不可能图形,这位荷兰籍的画家就是以画面中的数学性而闻名的,所以经常能在他的画中看到许多的数学概念,比如对称,分形和双曲几何等。
无尽的阶梯

无尽的阶梯又被称为彭罗斯阶梯,这是一个十分著名的几何悖论,描述的就是一个始终走不到头的台阶,可以无限的循环,就像彭罗斯三角形一样。这是1985年英国数学家彭罗斯提出的,这是高维空间才能实现的图形,所以不可能在三维空间中存在,就像克莱因瓶一样。
彭罗斯三角形

彭罗斯三角也是不可能图形中的一个,也是最纯粹的不可能图形,同样是由英国数学家彭罗斯设计并推广的,发表于1958年2月的《英国心理学期刊》上。整体看起来像是一个三角立体图形,但是仔细观察会发现,这个图形无法在三维中实现。
埃舍尔作品:不可能的世界

《瀑布》就是不可能的世界中的其中一个,一条瀑布从高处倾泻而下,转动着水轮,但是顺着水流慢慢向前,你却会发现水流竟然留到了瀑布的上方,之后又向下流去,这样周而复始,循环往复,形成一个既矛盾又有趣的画面。

《观景楼》也是不可能世界中的一个,整栋楼看似正常的排列,但是仔细观察就会发现,其中一个竖立的梯子它的最上面靠在观景楼的外边,但是最下面却伸进了观景楼的里面。
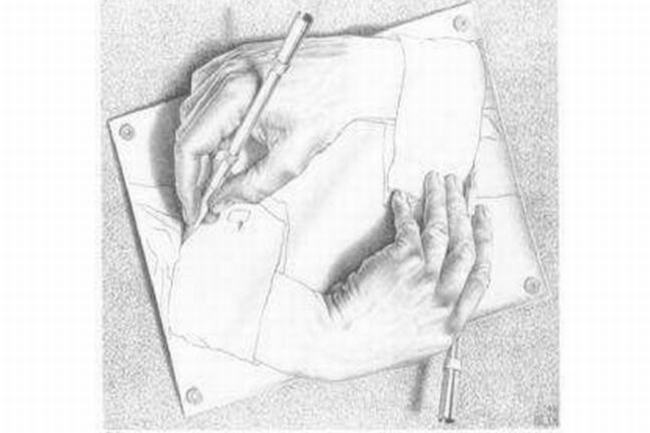
《画手》相信很多人都看过,一只手画着另一只手,让人分不成到底哪个才是真正的画。所有的一切仿佛都被固定在画中,但是又好像没有固定。
结语:不可能世界中还有很多不可能图形的体现,埃舍尔就是用这种独一无二的画法,让人印象深刻,空间的错乱让人不禁感叹数学的艺术美。
导语:彭罗斯阶梯是一个著名的悖论(几何学),指的是一个从始至终向上或者向下走不到尽头的楼梯,它永远无法找到最高或者最低的一点,该悖论是无法在我们生存的三维空间存在的。下面就跟着探秘志小编一起来看看彭罗斯阶梯吧!
彭罗斯阶梯是什么?
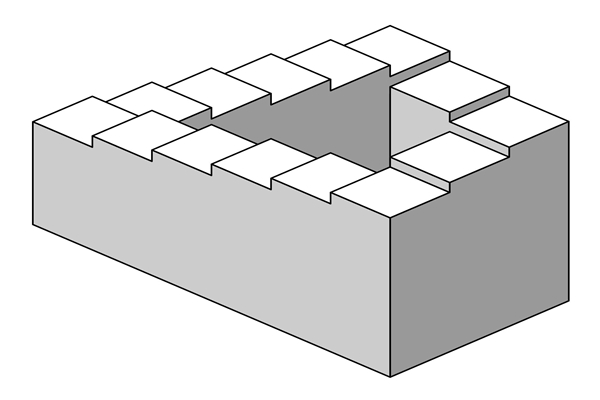
彭罗斯阶梯其实是数学中有名的几何学悖论,指的就是一个始终向下或向上但却永远走不到头的楼梯,彭罗斯阶梯其实是彭罗斯三角的变体,是1985年由英国数学家罗杰·彭罗斯和他的父亲一起提出的。
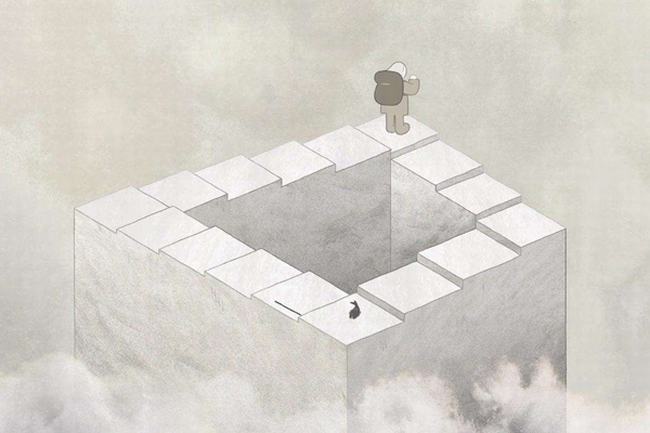
彭罗斯阶梯是由四条阶梯相连,在这个阶梯上永远也找不到最高的一点或最低的一点,所以人只能在同一个平面上打转转,在视觉上看似是相连的阶梯,却不能在现实中实现。荷兰画家埃舍尔就曾画过一系列的不可能世界,这与彭罗斯阶梯的原理很相似。
彭罗斯阶梯真实存在吗?

彭罗斯阶梯是著名的数学悖论,在理论上是真实存在的,但是在三维空间中并不能实现彭罗斯阶梯的构建,因为彭罗斯阶梯的这种不可能形体,只能放入更高维的空间中才能实现,而人类生活的三维世界还不能实现它,这就像莫比乌斯环和克莱因瓶的原理一样。

彭罗斯阶梯就是不可能图形中的一种,由于我们生活在三维世界,所以目前只能在二维图像中感受这一现象,但二维图像上的彭罗斯阶梯其实是一种视错觉,并不算真正意义上的彭罗斯阶梯。
彭罗斯阶梯常上荧屏

在盗梦空间中就曾出现过无尽楼梯,而现实中拍摄使用的楼梯也是找到一个合适的角度,才拍摄出了无限循环的效果。其实这段楼梯是分开的,但是由于摄像机的位置刚好将顶端和底部重合,所以让人看起来像彭罗斯阶梯一样,陷入了无限循环,感觉永远走不到头。

在鬼吹灯中的悬魂梯也是这样的效果,会把人困在其中,永远在里面打转无法走出。这个不可能阶梯虽然不能在现实中实现,但是也为人们展现出了数学的趣味所在。
结语:彭罗斯阶梯虽然不可能存在在现实中,但是也让人领略到了数学的魅力,就像画家埃舍尔的那些不可能的画一样。





