圆是初中几何的最后的压轴学习内容,它具有很多重要性质,知识的前后联系密切,能综合考查综合应用数学知识的能力,是历年中考必考的重点。特殊四边形主要包括平行四边形、菱形、矩形、正方形等,具有丰富的知识内涵,也是中考必考内容,特殊四边形与圆的组合探究问题充分体现数学知识之间的相互联系,能从中感受数学的整体性,体会在知识交汇处的命题特色,近年来中考试题往往将圆与四边形和相似形以及三角函数等多个知识点进行叠加,从而使问题具有较强的综合性,完美展现了直线型问题与曲线型问题的有机组合。尤其把观察、操作、证明融于一体,展示了数学探究的过程和方法,体现了对数学活动经验的关注,也体现了对培养学生发现和提出问题、分析和解决问题能力的关注.

类型1 平行四边形与圆的组合
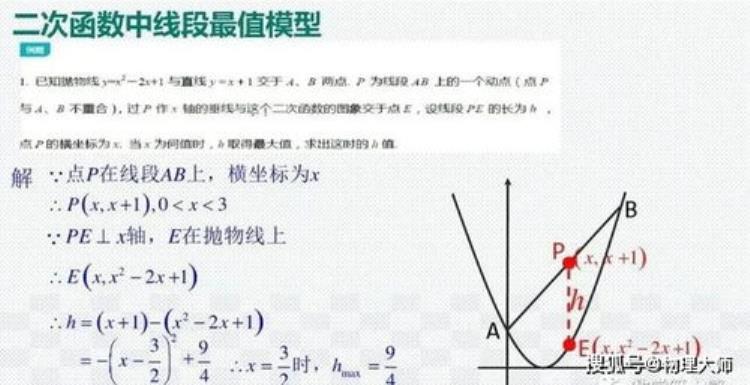
例1.(2018•南京二模)如图,在▱ABCD中,AB=3√2,BC=5,∠B=45°,点E为CD上一动点,经过A、C、E三点的⊙O交BC于点F.
【操作与发现】
(1)当E运动到AE⊥CD处,利用直尺与规作出点E与点F;(保留作图痕迹)
(2)在(1)的条件下,证明:AF/AE=AB/AD.
【探索与证明】
(3)点E运动到任何一个位置时,求证:AF/AE=AB/AD;
【延伸与应用】
(4)点E在运动的过程中求EF的最小值.
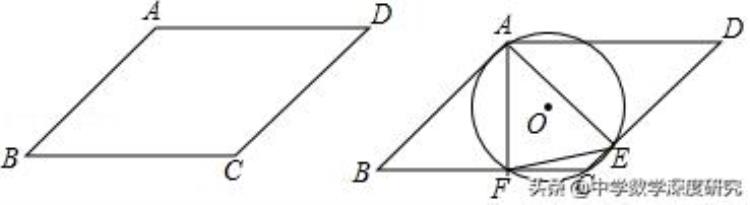
【分析】(1)当AE⊥CD,此时AC是⊙O的直径,作出AC的中点O后,以OA为半径作出⊙O即可作出点E、F;
(2)易知AC为直径,则AF⊥BC,S四边形ABCD=BC•AF=CD•AE,从而得证;
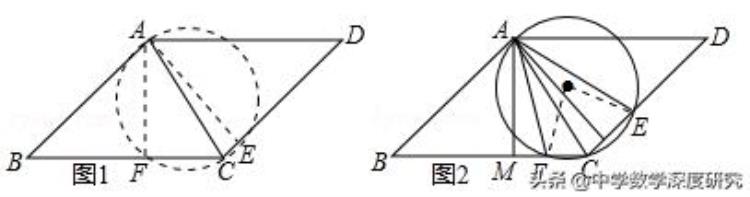
(3)如图,作AM⊥BC,AN⊥CD,若E在DN之间,由(2)可知,AM/AN=AB/AD,然后再证明△AMF∽△ANE,从而可知AM/AN=AF/AE=AB/AD,若E在CN之间时,同理可证;
(4)由于A、F、C、E四点共圆,所以∠FAE ∠BCD=180°,由于四边形ABCD为平行四边形,∠B=45°,从而可证△FOE为等腰直角三角形,所以FE=√2R,由于AN≤AC≤2R,所以E与N重合时,FE最小.
【解答】(1)如图1所示,
(2)如图,易知AC为直径,则AF⊥BC,则S四边形ABCD=BC•AF=CD•AE,
∴AF/AE=CD/BC=AB/AD.
(3)如图,作AM⊥BC,AN⊥CD,若E在DN之间
由(2)可知,AM/AN=AB/AD,
∵A、F、C、E四点共圆,∴∠AFC ∠AEC=180°,
∵∠AFC ∠AFM=180°,∴∠AEN=∠AFM,
∵∠AMF=∠ANE,∴△AMF∽△ANE,∴AM/AN=AF/AE=AB/AD,
若E在CN之间时,同理可证
(4)∵A、F、C、E四点共圆,∴∠FAE ∠BCD=180°,
∵四边形ABCD为平行四边形,∠B=45°,∴∠BCD=135°,
∴∠FAE=45°,∴∠FOE=90°,∴△FOE为等腰直角三角形,∴FE=√2R
∵AN≤AC≤2R,∴E与N重合时,FE最小,此时FE=√2/2AC,
在△ABC中,AM=BM=3,则CM=2
∴由勾股定理可知:AC=√13,此时EF最小值为√26/2
【点评】本题考查圆的综合问题,涉及相似三角形的性质与判定,平行四边形的性质与判定,等腰三角形的性质,尺规作图等知识,综合程度较高,需要学生灵活运用所学知识.解题时要先分析题干中的条件,然后从图象中挖掘隐含条件,最后再解题.

类型2 矩形与圆的组合
例2.(2018•宿迁三模)如图,在矩形ABCD中,AB=6,AD=8,动点E、F同时分别从点A、B出发,沿着射线AD、射线BD的方向均以每秒1个单位的速度运动,连接EF,以EF为直径作⊙O交射线BD于点M,设运动时间为t.
(1)当点E在线段AD上时,用含字母t的代数式表示DE、DM的长;
(2)在运动过程中,连接CM,当t为何值时,△CDM为等腰三角形.
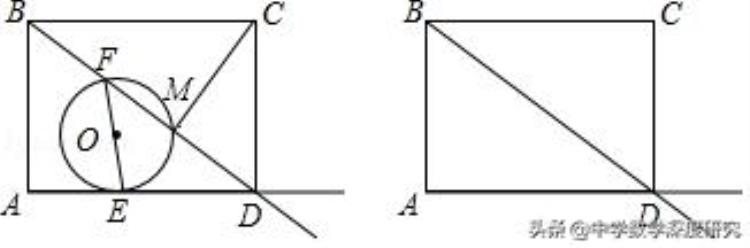
【分析】(1)由题意可得DE=8﹣t,由cos∠ADB=AD/BD=DM/DE,可求DM=4/5(8﹣t);
(2)利用分类思想讨论,分MC=MD,MC=CD,MD=CD三种情况讨论,再根据锐角三角函数求t的值.
【解答】(1)如图1:连接EM.
∵AB=6,AD=8,∴利用勾股定理,可得BD=10;
∵AD=8,AE=t,∴DE=AD﹣AE=8﹣t;
∵EF是直径,∴∠EMF=90°;
∵cos∠ADB=AD/BD=DM/DE,∴8/10=DM/8-t,∴DM=4/5(8﹣t);
(2)①当DM=CD=6时,∴DM=4/5(8﹣t)=6,∴t=1/2;
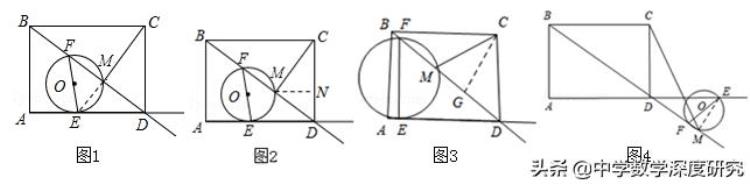
②如图2,过点M作MN⊥CD.
当MC=MD时,
∵MC=MD,MN⊥CD,∴CN=DN=3;
∵AB∥CD,∴∠ABD=∠BDC,∴cos∠ABD=cos∠BDC=AB/BD=DN/MD,
∴6/10=3/MD,∴MD=5,∴DM=4/5(8﹣t)=5,∴t=7/4;
③当MC=CD=6时,
如图3,过点C作CG⊥BD,
∵MC=CD,CG⊥BD,∴GD=MG;
∵cos∠ABD=cos∠BDC=AB/BD=GD/CD,∴6/10=GD/6,
∴GD=3.6,∴MD=7.2,∴4/5(8﹣t)=7.2,∴t=﹣1(不合题意舍去);
④当CD=DM=6时,如图4.
∵AE=t,AD=8,∴DE=t﹣8;
∵∠BDA=∠EDM,∴cos∠BDA=cos∠EDM=AD/BD=DM/DE,
∴8/10=6/(t-8),∴t=31/2.
综上所述:当t=1/2或t=7/4或t=31/2时,△CDM为等腰三角形.
【点评】本题考查了圆的综合题,等腰三角形的性质,锐角三角函数,利用分类思想讨论解决问题是本题的关键.

类型3 菱形与圆的组合
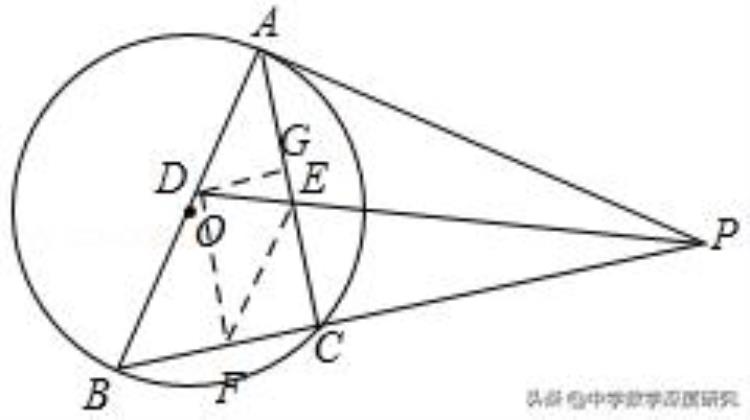
例3.(2018•淄博中考题)如图,以AB为直径的⊙O外接于△ABC,过A点的切线AP与BC的延长线交于点P,∠APB的平分线分别交AB,AC于点D,E,其中AE,BD(AE<BD)的长是一元二次方程x ²﹣5x 6=0的两个实数根.
(1)求证:PA•BD=PB•AE;
(2)在线段BC上是否存在一点M,使得四边形ADME是菱形?若存在,请给予证明,并求其面积;若不存在,说明理由.
【分析】(1)易证∠APE=∠BPD,∠EAP=∠B,从而可知△PAE∽△PBD,利用相似三角形的性质即可求出答案.
(2)过点D作DF⊥PB于点F,作DG⊥AC于点G,易求得AE=2,BD=3,由(1)可知:PA/2=PB/3,从而可知cos∠BDF=cos∠BAC=cos∠APC=2/3,从而可求出AD和DG的长度,进而证明四边形ADFE是菱形,此时F点即为M点,利用平行四边形的面积即可求出菱形ADFE的面积.
【解答】:(1)∵DP平分∠APB,∴∠APE=∠BPD,
∵AP与⊙O相切,∴∠BAP=∠BAC ∠EAP=90°,
∵AB是⊙O的直径,∴∠ACB=∠BAC ∠B=90°,∴∠EAP=∠B,
∴△PAE∽△PBD,∴PA/AE=PB/BD,∴PA•BD=PB•AE;
(2)过点D作DF⊥PB于点F,作DG⊥AC于点G,
∵DP平分∠APB,AD⊥AP,DF⊥PB,∴AD=DF,
∵∠EAP=∠B,∴∠APC=∠BAC,易证:DF∥AC,∴∠BDF=∠BAC,
由于AE,BD(AE<BD)的长是x ²﹣5x 6=0,解得:AE=2,BD=3,
∴由(1)可知:PA/2=PB/3,
∴cos∠APC=PA/PB=2/3,∴cos∠BDF=cos∠APC=2/3,
∴DF/BD=2/3,∴DF=2,∴DF=AE,∴四边形ADFE是平行四边形,
∵AD=AE,∴四边形ADFE是菱形,此时点F即为M点,
∵cos∠BAC=cos∠APC=2/3,∴sin∠BAC=√5/3,
∴DG/AD=√5/3,∴DG=2√5/3,
∴在线段BC上是否存在一点M,使得四边形ADME是菱形
其面积为:DG•AE=2×2√5/3=4√5/3
【点评】本题考查圆的综合问题,涉及圆周角定理,锐角三角函数的定义,平行四边形的判定及其面积公式,相似三角形的判定与性质,综合程度较高,考查学生的灵活运用知识的能力.

类型4 正方形与圆的组合
例4.(2018秋•泰兴市校级月考)如图,已知正方形ABCD的边长为4,点P是AB边上的一个动点,连接CP,过点P作PC的垂线交AD于点E,以PE为边作正方形PEFG,顶点G在线段PC上,对角线EG、PF相交于点O.
(1)若AP=1,则AE=_______ ;
(2)①求证:点O一定在△APE的外接圆上;
②当点P从点A运动到点B时,点O也随之运动,求点O经过的路径长;
(3)当点P运动至AB中点时,求线段CO的长.
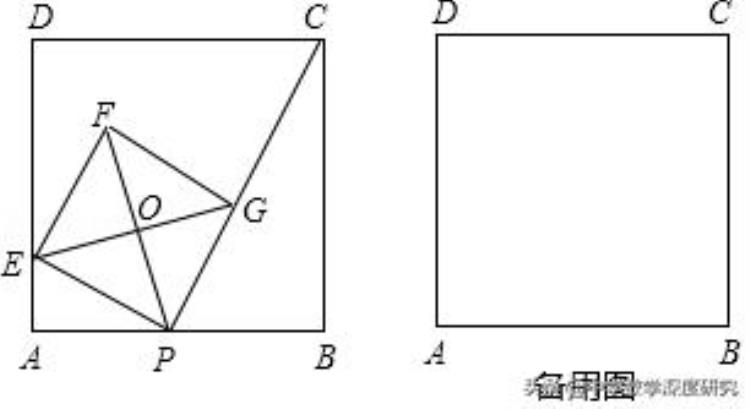
【分析】(1)由正方形的性质得出∠A=∠B=∠EPG=90°,PF⊥EG,AB=BC=4,∠OEP=45°,由角的互余关系证出∠AEP=∠BPC,得出△APE∽△BCP,得出对应边成比例即可求出AE的长;
(2)①求证A、P、O、E四点共圆,即可得出结论;
②连接OA、AC,由勾股定理求出AC=4√2,由圆周角定理得出∠OAP=∠OEP=45°,周长点O在AC上,当P运动到点B时,O为AC的中点,即可得出答案;
(3)连接AC,易知AC过点O,运用勾股定理求出AE,OP,CP的值,进而运用△APE∽△BCP,列出相关比例线段求解即可.
【解答】(1)∵四边形ABCD、四边形PEFG是正方形,
∴∠A=∠B=∠EPG=90°,PF⊥EG,AB=BC=4,∠OEP=45°,
∴∠AEP ∠APE=90°,∠BPC ∠APE=90°,
∴∠AEP=∠BPC,∴△APE∽△BCP,
∴AE/BP=AP/BC,即AE/(4-1)=1/4,解得:AE=3/4,故答案为3/4;
(2)①证明:如图1,取PE的中点Q,连接AQ,OQ,
∵∠POE=90°,∴OQ=1/2PE,
∵△APE是直角三角形,∴点Q是Rt△APE外接圆的圆心,∴AQ=1/2PE,∴OQ=AQ,
∴点O一定在△APE的外接圆上;(到圆心的距离等于半径的点必在此圆上)
②解:连接OA、AC,如图1所示:
∵四边形ABCD是正方形,∴∠B=90°,∠BAC=45°
∴利用勾股定理可求得AC=4√2,
∵A、P、O、E四点共圆,∴∠OAP=∠OEP=45°,∴点O在AC上,
当P运动到点B时,O为AC的中点,OA=1/2AC=2√2,
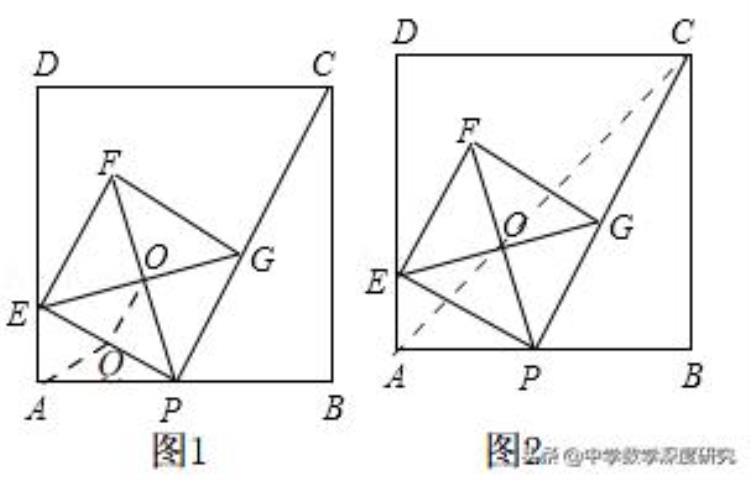
(3)如图2连接AC,由(2)知AC经过点O,且∠CAO=∠OPC=45°,
又∵∠ACP=∠OCP,∴△COP∽△CPA,∴CO/CP=OP/AP,
点P运动至AB中点时,AP=BP=2,
由(1)知△APE∽△BCP,
∴AE/BP=AP/BC,∴AE/2=2/4,解得:AE=1,
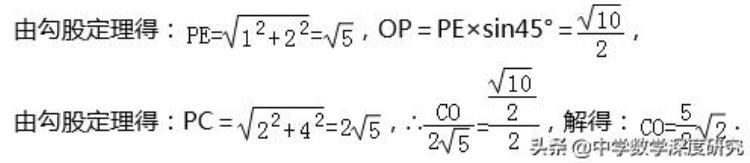
【点评】此题是圆的综合题目,考查了正方形的性质、四点共圆、圆周角定理、三角形的外接圆、相似三角形的判定与性质、勾股定理等知识,综合性强,难度较大.

类型5 新定义四边形与圆的组合
例5.(2018•秦淮区一模)【数学概念】
若四边形ABCD的四条边满足AB•CD=AD•BC,则称四边形ABCD是和谐四边形.
【特例辨别】
(1)下列四边形:①平行四边形,②矩形,③菱形,④正方形.其中一定是和谐四边形的是_______ .
【概念判定】
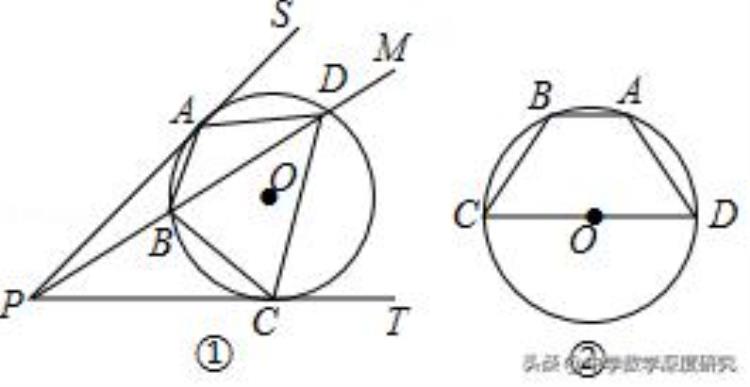
(2)如图①,过⊙O外一点P引圆的两条切线PS、PT,切点分别为A、C,过点P 作一条射线PM,分别交⊙O于点B、D,连接AB、BC、CD、DA.求证:四边形ABCD是和谐四边形.
【知识应用】
(3)如图②,CD是⊙O的直径,和谐四边形ABCD内接于⊙O,且BC=AD.请直接写出AB与CD的关系.
【解析】(1)如图1,
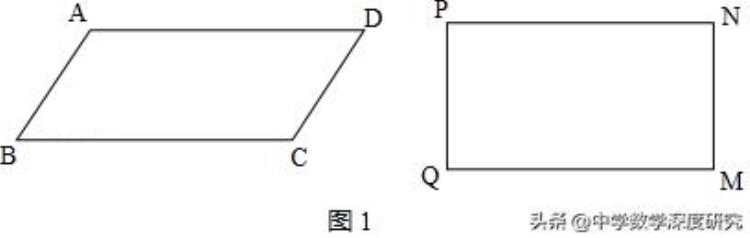
若▱ABCD为和谐四边形,则AB•CD=AD•BC,
∵AB=CD、AD=BC,∴AB ²=BC ²,即AB=CD,
则▱ABCD为菱形;若矩形PQMN为和谐四边形,则PQ•MN=PN•QM,
∵PQ=MN、PN=QM,∴PQ ²=QM ²,即PQ=MN,则矩形PQMN是正方形;
∴一定是和谐四边形的是菱形和正方形,
故答案为:③④.
(2)如图2,连接CO并延长,交⊙O于点E,连接BE.
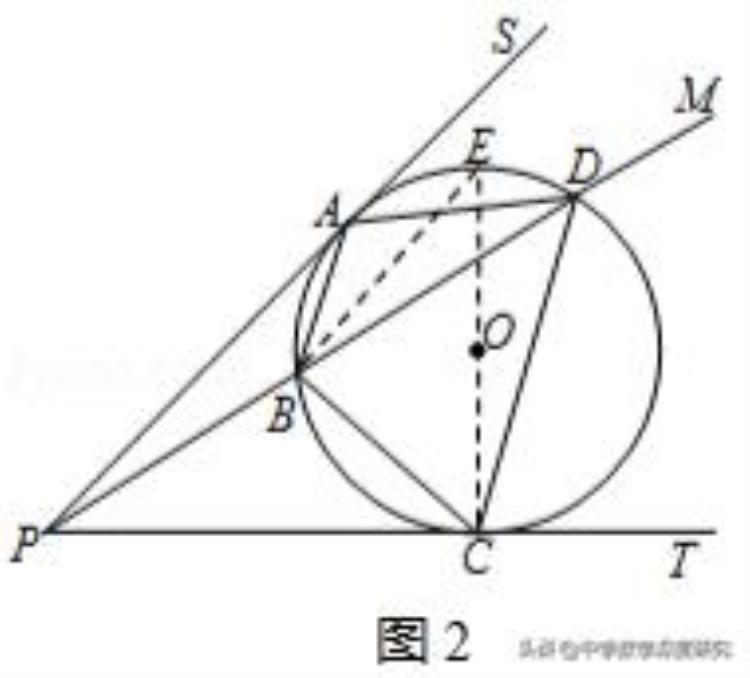
∵PT是⊙O的切线,切点为C,∴∠PCE=90°.∴∠PCB ∠ECB=90°.
∵CE是⊙O的直径,∴∠CBE=90°,∴∠BEC ∠ECB=90°,∴∠BEC=∠PCB.
又∵∠BEC=∠BDC,∴∠PCB=∠BDC.
又∵∠BPC=∠CPD,∴△PBC∽△PCD,∴CB/CD=PC/PD.同理,AB/AD=PA/PD.
∵PA、PC为⊙O的切线,∴PA=PC,∴CB/CD=AB/AD.∴AB•CD=AD•BC.
∴四边形ABCD是和谐四边形.
(3)如图3,连接BD、作BE⊥CD于点E,
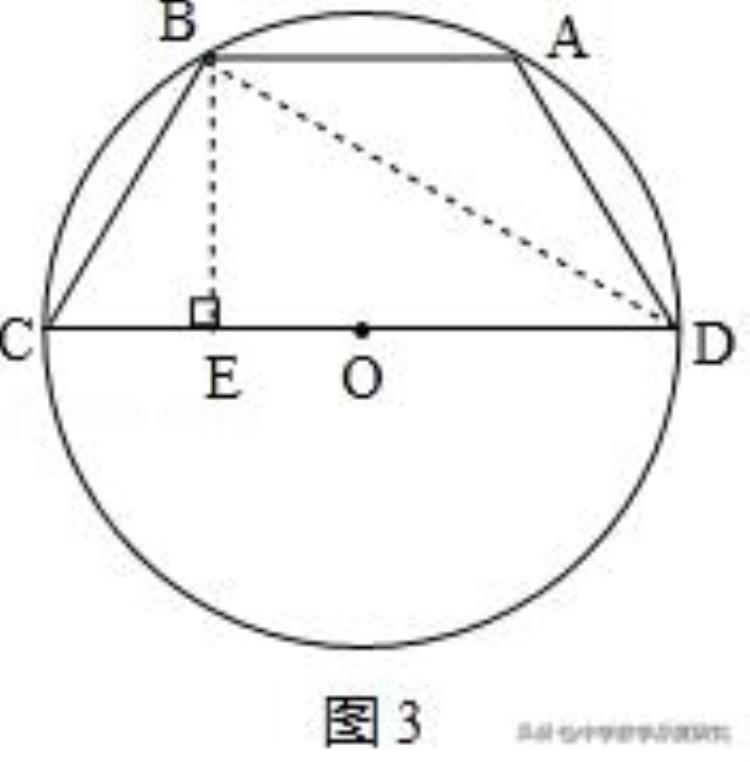
∵BC=AD,∴弧BC=弧AD,∴∠CDB=∠ABD,则AB∥CD,
∴四边形ABCD是等腰梯形,
设BC=AD=a、AB=x、CD=y,则CE=(CD-AB)/2=(y-x)/2,
∵CD为⊙O的直径,∴∠CBD=∠CEB=90°,
又∠C=∠C,∴△CBE∽△CDB,则CB/CD=CE/CB,

【点评】本题主要考查圆的综合问题,解题的关键是熟练掌握与圆有关的概念和性质、对新定义的理解、应用,相似三角形的判定与性质,等腰梯形的判定与性质等知识点的运用.

综上所述,圆与特殊四边形的综合探究题灵活多变,看似无固定的解题模式或套路.但解决这类问题的方法:一是根据条件,结合已学的知识、数学思想方法,通过分析、明确圆与特殊四边形知识衔接,逐步得出结论,或通过观察、实验、猜想、论证的方法求解;二是关注前面几个小题在求解过程的解题思路和方法,会对最后一小题的求解有一定的借鉴作用,还可以把前面几个小题的结论作为已知条件,为最后一问的求解提供帮助.经过一定量题目训练及反思,我们一定会掌握这类问题求解。
提醒一点:解与圆有关的几何问题时,常常需要添加适当的辅助线将复杂的图形转化为基本图形,从而方便求解,平时要加强对辅助线的学习积累。在平面几何中,解决与圆有关的问题时,常常需要添加适当的辅助线,架起题设和结论间的桥梁,从而使问题化难为易,顺其自然地得到解决,如有关弦的问题,常作其弦心距(有时还须作出相应的半径),通过垂径平分定理,来沟通题设与结论间的联系。在题目中若已知圆的直径,一般是作直径所对的圆周角,利用"直径所对的圆周角是直角"这一特征来证明问题。命题的条件中含有圆的切线,往往是连结过切点的半径,利用"切线与半径垂直"这一性质来证明问题。

教育界流行一句这样的话:不论学校教育,还是家庭教育,甚至社会教育,最大的成功在于想尽一切办法后能最大化地激起受教育者自育自悟自成,我们就要做这样做的人。
真心真情真东西,讲究提供最新鲜最实用考试素材。原创不易,期待你的关注,留言,分享,转发,点赞,相互促进,共同提高数学成绩。

初中数学圆和四边形的证明题有什么方法?
首先把书上的 定理理解记忆 ,注意是要理解,(所以首先你自己问下自己是不是都理解了的 ,)在在题型做去应用 ,另外 ,这2种证明题的出题模式都是有限的 ,反正就是考你书上的定理 ,做题的时候,两种思维方式做第一种:由结论出发 ,我们先找要得到这个结论,需要什么条件 ,看看这些需要的条件是不是都已知,对于那些不知道的,那么我们由去找,要使它成为已知又不许要什么条件,最后需要的条件刚好都是已知的。(这种方法叫反证法?
第二种:有已知条件出发 ,已知条件,加上各样的定理,看看能推出那些已知条件,已知条件就增加了 ,在组合,由推出其他已知条件,知道能推出需要证明的结论
初中数学圆的解题技巧,全面一点,实用一点。
首先要灵活记号和使用书上介绍的定理及其推论,比如看到弦和直径要马上想到垂径定理,外加补充相交弦定理和弦切角定理,这两个用在填空选择上比较理想,能有效提高解题速度,有兴趣查一下。大题的话也可以直接使用。如果在综合题中圆一般用来找等腰三角形,还有以直径为一边的圆内接三角形是直角三角形,内接平行四边形是矩形(好像是,记不清了),经常作为隐含条件。圆的类型题太多了,没法说的全面,我也是才疏学浅,希望能帮到你。




