贝特朗曾经在1899年提出了一个悖论就是,假设一个内接圆的等边三角形中,任意选择一条弦,那么这条弦长于等边三角形边长的几率有多大?但结果却并不是唯一的,分别利用三种方法解答出了二分之一、三分之一和四分之一,可以说它们都完全正确但相互矛盾,因此就形成了一个悖论。
贝特朗悖论正确答案
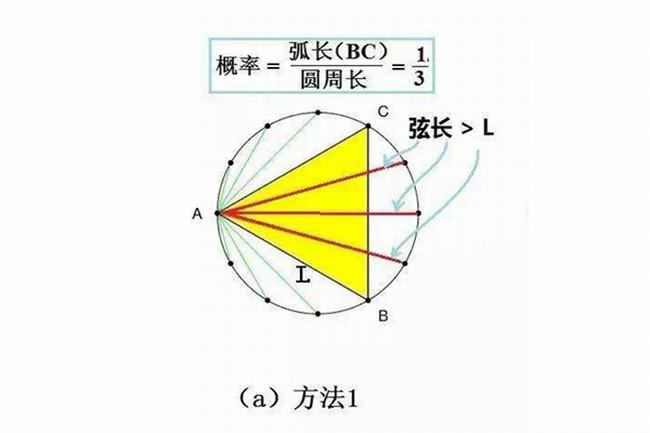
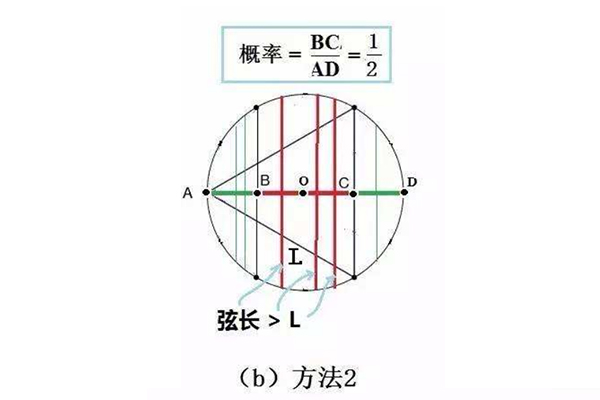
贝特朗悖论中并没有规定弦的位置、方向等,所以一共可以分为三种情况进行解答,第一种解法是先预设弦的方向,可以做出垂直于这条弦的直径,而计算出只有交于直径的四分之一和四分之三处的弦才是等于边长的,因此计算出概率为二分之一。而第二种方法则是预设了弦的一端,只有当弦与这个端点的切线交角为60-120度的时候才能等边,而概率就是三分之一。
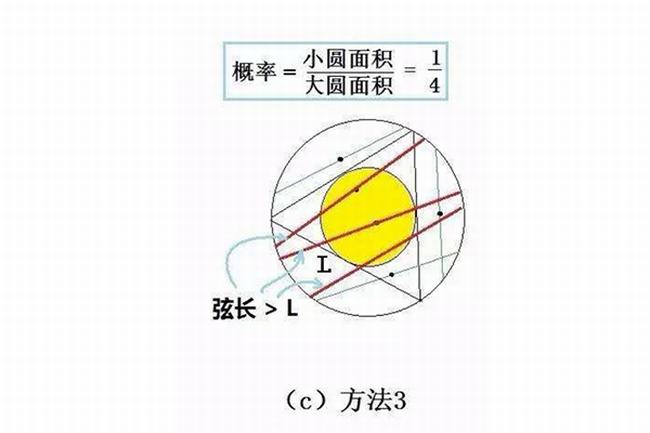
当然还有第三种解法,也是目前课本中最常用的解法,主要是根据弦的中点来看,只有弦的中心点能够落在比本圆半径小一半的同心圆上就能等长,因此这时的概率则只有四分之一。所以三种结果都不相同,但几乎都没有计算错误,其实也都是因为它的前提是不同的,在出题的时候,其中等可能”的词汇会产生误导,这其实和芝诺悖论有得一拼。
贝特朗悖论的类似解释
其实这一悖论就是最初贝特朗用来反思几何学运算概率学到底是否合适的,其实这一悖论还有另外的一种版本。假设有1、2、3号箱子,其中1号有2根金条,2号有两根银条,3号有1根金条1根银条,打开一个隔间是金条,而打开另一个隔间也是金条的概率有多少?相信一般人都会认为是二分之一。

但实际上正确答案却是三分之二,因为我们可以看到2号箱子中只有银条,所以可以立即将它排除掉,而只剩下另外的1号和3号是有可能的,所以总的来说应该是三个箱子中有两个是可能的,所以这也是贝特朗悖论中最为简单的一个理解方式。
古希腊哲学家芝诺其实提出了不少的悖论,其中最著名的四个分别是二分法悖论、阿基里斯悖论、飞矢不动悖论以及竞走悖论,这些悖论几乎都是想要争论世界上的时空到底是可分的还是不可分的,如果可分,那么第一和第三个悖论就无法解决,而如果空间是不可分的,则第三个无法解决。
芝诺悖论是什么1. 二分法悖论
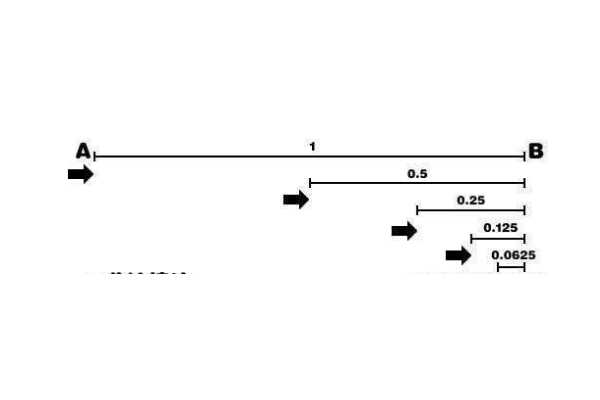
如果假设一个人从A走到B,那么他就一定要通过中心点C,而如果他要从A走到C,那么就一定要通过中心点D,而以此类推下去,那么也就意味着他不管怎么走,都必须要走到中心点,但中心点也就意味着他一定会距离终点有一定的距离,因为哪怕这段距离再小也能找到中心,所以这就使得他形成了一个永远也走不到终点的神奇悖论。
2. 阿基里斯悖论
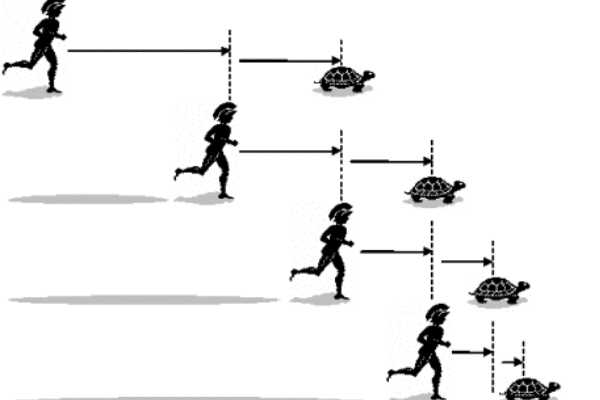
假设古希腊跑的最快的人阿基里斯和一只乌龟进行赛跑,那么首先他就要追上乌龟跑过的第一个位置,当他到位之后,乌龟这时就已经走到第二个点,那么以此类推下去,阿基里斯几乎永远也没有可能追上乌龟,但实际上这时不可能的,因此便形成了第二个悖论。
3. 飞矢不动悖论

当一只箭射出之后,人们看起来它是运动的,但飞箭在某一个瞬间实际上又是不动的,那么人们就会陷入一种飞箭动与不动的争论之中,因此这一悖论就是和“运动可分”这一观点相联系的。
4. 竞走悖论

这一悖论的前提也是时空是有限可分的,假设有三个点A、B、C,其中C向着右边移动,而A向着左边移动,它们的速度对于B来说就是每瞬间移动一个点,而这就意味着A的每点在每个瞬间都会离开C两个点移动的距离,从而我们就能将其无穷化,最终就得出了时间不可分的结论,与前提冲突。